17/01/2025
Wandee's Blog
Revisiting the One-Time Pad
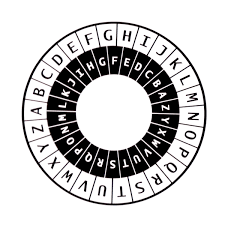
Alberti Disk and One-Time Pad
Leon Battista Alberti invented in the 15th century the disk named after him (Alberti Disk). Kahn (The Codebreakers by David Kahn) refers to it as the point in time when polyalphabetical ciphers had been invented. For an experiment we place on the inner disk of the Alberti Disk a permutation of the English alphabet. The inner disk can be moved clockwise or anti clockwise and assuming that the start is at the top (0 degree), we have 26 possible permutations at our disposal to map an English text. Each permutation presents a different alphabet when used for encrypting plaintext via mapping. Very easy to explain and prove by looking at the English alphabet where the order of characters is A to Z (first permutation of 4.032915e+26 possible permutations). Here the order and frequencies of characters generate character strings (Words, sentences etc.), which for us translate into meaningful data (Example: HELLO). Let's change the order of characters in the alphabet and map the word HELLO twice against two different permutations.

With the first mapping the ciphertext we get is TVRRB and with the second PTBBE. We don't need the help of a cryptologist to figure out that we only have a limited amount of five character words in the English language, which after mapping against a single permutation of the alphabet would create pattern like these (notice the double character). Before we look further at permutations (English alphabet)*1) let's take a look at Shannon's proof for achieving perfect secrecy for the One-Time Pad. Shannon uses the English alphabet, but any other alphabet will work as well, with a fixed character set. Shannon doesn't use a mapping process, but instead selects randomly characters from the alphabet, which then are paired with the plaintext characters using modular arithmetic. Shannon was aware that a plaintext was not a collection of random characters *2), but required for a meaningful text a structure with different frequencies for characters and pattern (E/e for example is the character with the highest frequency in the English language and pattern like th, ll, oo, er etc are common). If we only have a limited amount of key characters and the message length exceeds the amount, it is unavoidable that frequencies and pattern will slip into a ciphertext (see the two mapping results we produced, which clearly identify a double character). Shannon's solution for the Vernam cipher (today's OTP) stated that RMLM ≤ RKLK was required to maintain perfect secrecy,*3) else his entropy (H) function would provide the tool to break a ciphertext. Shannon's solution suggested a Markov (Markoff) process which would generate an infinite amount of unique random symbols which could be paired with the message characters, ensuring that that RMLM ≤ RKLK was always present.
Let's take a look at Shannon's Entropy and what it tells us:
Shannon's Entropy
Shannon's axioms explaining function H
to be a measure of a message A and the information it contains:
1. It should be continuous in the P(ai), where P is a probability.
2. It increases monotonically with N if P(ai) = 1/N
3. It satisfies the decomposition rule for joint entropy of two discrete random variables.
Shannon's entropy is build on an assumption, a very, very strong assumption indeed. The expression measure means by definition, that we have something, a property, that can be measured in its own right. For Shannon that meant a coherent text in English (or any other language), as long as the statistical values he needed for his entropy function were present. How he gained his entropy values are explained in his papers.*4) *6) To support Shannon's entropy, we will find in many publications the key equivocation H(K|Cn), which measures the remaining entropy (uncertainty) in the key. For this to work we require a n-gram of ciphertext, enabling us to obtain the unicity point, which is the smallest point of a cryptosystem giving us H(K | Cn) ≈ 0. With that we could claim that there is an average ciphertext length, which has only one key that can create a meaningful message.
What do these three axioms tell us, when the plaintext isn't a property, that in its own right can be measured? We told AIs (Leo-Brave Browser, ChatGPT, DeepSeek and others) that the message (plaintext) has changed from a property that can be measured into a random string of data; with RMLM > RKLK. The question we asked :
Let's assume we have a plaintext string of random characters and a key string that only consists of 26 characters. The plaintext uses the same alphabet as the key string, but is 10.000 random characters in length. How would an attacker try to crack a cipher created, using modular arithmetic and what would be the result of this attempt?
Most readers will come to the conclusion that an attacker will have to go through all possible character combinations, when faced with a cipher generated this way. Each character and that applies to plaintext and key has a probability of 1/26, meaning each position is a single OTP were N = 1 as far as the plaintext is concerned. Of course AIs didn't see it this way at the start of our exchange. For people working in cryptology and mathematicians we asked it was not a problem. However, they asked the sensible question what use a random plaintext would be for an intended recipient. We will answer that question further down, but first look at the AI systems and their responses.
All systems started to preach the mantra, that can be found on the Internet or publications dealing with the One-Time Pad. That a key string which would be less in length than the plaintext lead to pattern in the cipher and these could be explored by an attacker. Human Intelligence didn't have a problem with understanding the question and realizing that a random string paired with another random string doesn't generate pattern or frequencies that will make sense to us; or permit us from the cipher to predict the outcome of any of the modular arithmetic steps, when looking at the cipher characters.
So, we ask all AI systems to provide us with an example that would be proof for Random + Random = Predictable and disprove our Theorie that Random + Random ≠ Predictable. To emphasize our point we mentioned that each plaintext and key character had a probability of 1/26 and hence each plaintext character was a N = 1 situation. We also added the three points below to clarify Shannon's three axioms.
1a.)
The first axiom is true only if we stay in the same language (continuous in the P[ai]), where the rules that permit to generate a coherent and meaningful message will not change (In the English language these are the characters from A to Z, frequencies of characters, pattern etc).
2a.)
The second axiom is true if the first axiom is true and RMLM ≤ RKLK. Else the monotonically increase with N is only present as long as we have a unique key for each N, otherwise N ≠ 1 anymore. Shannon says about it: "With N = 1 any letter is clearly possible and has the same a posteriori probability as its a priori probability. For one letter the system is perfect".
3a.)
If axiom one or axiom two are not true, axiom three cannot be true (decomposition rule), because it relies on the two previous axioms.*5)
At this point all systems still maintained that a short key used for a long text of randomly selected characters would still develop pattern and frequencies that would enable an attacker to crack a cipher. For that reason we rephrased our question and stating that we have a random string of charters (plaintext) without pattern or frequencies that match the English, Dutch or any other language using the same alphabet. The possible key characters would be the 28 (we added a space character and fullstop to the english alphabet) characters as seen in the example. How would an adversery know or detect that we only have used a single key character or two or more to match the plaintext characters?
0ne AI (Leo) was now willing to accept that a brute force attack would be required to crack the cipher and that all possible decryptions could be the plaintext. ChatGPT (the other AIs had similar problems, but without the need to repeat the question we had asked) seemed to have a problem with it, because it started with a reply, but stopped after six words without continuing the sentence it started. After repeating the question it finally came to the same conclusion, but not without pointing out that the applied key had to be random and that the key should be distributed without repetition of a character. It appears that the event horizon around the black hole, which is the data they have collected is flawed. Not a reply that is based on independent thinking and is missing any logical approach.
Let's look now at the answer we provided to the people who had problems with a random character string as plaintext and the usefulness of it.
A Hypothetical Experiment
For our experiment we assume that two trained chimpanzees hammering away on two typewriters. The first output will be our plaintext (naturally meaningless random characters) and the second output our key characters, also meaningless. Using modular arithmetic, we create a ciphertext, based on these two character strings. Our question is how much n-gram of ciphertext is required to measure the uncertainty in the key and do we actually reach a unicity point? Stupid question you might think, but nevertheless it proves that Shannon's entropy depends on a property (plaintext), which in its own right can be measured. We can carry on with the experiment until judgement day and no amount of ciphertext would allow to predict plaintext or key.
We were looking for a system, which would provide us with a N = 1 solution for each character after transformation of a meaningful plaintext. Looking into the past, the only system appealing to us was the Enigma machine used by the Germans during WWII. The flaws it had could be easily rectified, giving us a N = 1 randomized plaintext. Instead of using 3, 4, 5 or 8 permutation of an alphabet we have all permutations of the alphabet available, meaning each original plaintext character could be mapped against a unique permutation character.
The suggestion (someone mentioned it) that a Turing test might be able to crack our ciphers, we will put to the test here. Two examples, each encrypting a five letter word.
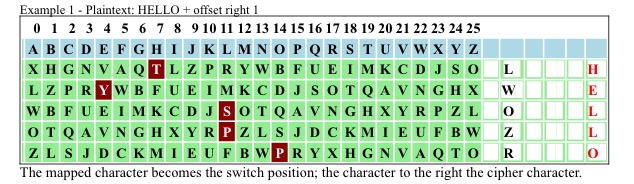
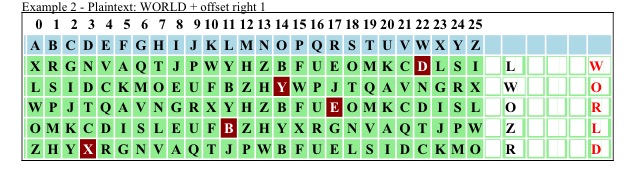
We have two equal ciphertext results achieved with two different plaintext words by simply changing our start permutations. Each plaintext character has its own permutation for the mapping process. This gives us a N = 1 solution with a 1/26 probability for each character. Now let's add a random key after each mapping step.
(m → tm) | ci = tmi + ki | mod 26

The mathematics on it is easy. We use the enigma process to change our message (m) into a transposition message (tm) and select a column to provide us with random characters for the key (k)(V - 21). From here onwards we proceed like we would with OTP encryption and pair tm with k via modular arithmetic to gain c.
Anybody now trying to solve the problem with math will have a problem. Let's take a look why a Turing test and Shannon's entropy (H)*6) test will fail to produce a single string that would provide the random cipher string, which then could be tested to lead to the original plaintext.
We have to compare the permutations the Enigma used (3,4 and 5) and the permutations in our system (P!26). Alan Turing and his team had to deal with a limited amount of permutations and the fact that these permutations (rotors in the Enigma) were not changed after each message, but used for the duration of a day and the Germans even failed to do this on occasions. With that a large amount of messages (text) was available to determine the settings of the alphabet on each rotor and to check for patterns and frequencies that occur when language *7) is used.
Shannon's entropy provides the clue when looking at an alphabet and what happens when the same characters are used as key characters. Shannon puts the amount of cipher text required at about 52 characters, when entropy drops and it becomes possible to crack a cipher created by using modular arithmetic [ 1a, 2a in the text above ]. Alan Turing faced the same problem, but that he not only had one alphabet to deal with, but three, four, five and probably eight alphabets (permutations). Each rotor added by the Germans made it more difficult to identify the single alphabets and the sequence of characters on these rotors.
Here we will leave it and readers intrested in the OTP can find on the Internet Shannon's papers. We will move to the permutations on the next page [Examples] and see if they offer a better solution for OTP encryption.
Conclusion
In the 17th century Isaac Newton wrote a letter to Robert Hooke, using a metaphor why he was able to find the laws of gravity. He wrote: "If I have seen further it is by standing on the shoulders of Giants". The problem with it is that we might see further, but we miss the small obstacles in front of the giant, which a giant can step over with ease, but would force us to take a different direction and path to reach our destination. So we stepped off the shoulders that gave us today's OTP and looked at the first obstacle. It was not the key, but the plaintext we stumbled on and it was easier to remove frequencies and pattern, than creating a key which had to be unique for each plaintext character.
*1)
Possible Permutations: P!26 = 4.032914611 x 1026 = 403,291,461,100,000,000,000,000,000.
*2)
It was first mentioned in written records over 1100 years back by a mathematician, who went by the name of Al Kindi. He lived in the Middle East in the region close to Damascus. He noticed that replacing plaintext characters with random characters in a large enough message text would develop recognizable pattern in a ciphertext, which could be used to restore the plaintext. Language tools in cryptology like frequency analysis, pattern recognition etc go all back to that time, however, his writings were lost and only rediscovered in the late 1980's. But it was Claude Shannon, who in the 1940s developed the mathematics that would be used to look at ciphertexts and find the connections between ciphertext and plaintext. It became known as Shannon's Entropy or expressed by the character H.
*3)
A Mathematical Theory of Communication by C.E. Shannon - The Bell System Technical Journal, Vol. 27, pp. 379-423, 623-656, July, October, 1948. | Online Link: A Mathematical Theory of Communication
RM = alphabet for message characters; RK = alphabet for key characters; LM = message length; LK = key length; ≤ = equal or less than;
This means if RM = RK (message alphabet and key alphabet are the same or hold the same amount of available characters) the message length can not exceed the amount of characters in the alphabet and LM > KM would allow theoretically to break a cipher
*4)
Shannon, Claude E.: Prediction and entropy of printed English, The Bell System Technical Journal, 30:50-64, January 1951
*5)
Comments about Shannon's entropy (H).
Shannon's Entropy has been published over 70 years ago, but the discusion about it and its validity is still ongoing.
1. Kahre, J (2002) The Mathematical Theory of Information, Kluwer: Dordrecht.
The belief in entropy as the only adequate measure of information is deeply rooted. This can be seen in the information theory literature, where the uniqueness of H is proved in different ways using the same basic method. A set of axioms is proposed and declared to be necessary for an information measure, and then the "uniqueness theorem" is proved, i.e. that H is the only function satisfying the proposed axioms...These properties are rather strongly tailored to the Shannon entropy (Aczel and Daroczy 1975). Hence the proofs have a flavour of circularity. The goal seems to be to find the weakest possible set of axioms (Gottinger, 1975 p.7-8) sufficient to prove the uniqueness of H. (Page 107).......
The axioms 1-3 cannot however, be accepted as fundamental properties of an information measure, because many important information measures are in conflict with the axioms. For instance, members of the utility family such as Gambler's gain, or reliability, violate the decomposition rule. (Page 108)
Decomposition rule: H(A,B) = H(A) + H(B | A)
= H(B) + H(A | B)
= H(A) + H(B) if A and B are independent random variables.
*6)
With the assistance of his wife and a friend, Shannon created his entropy. They had to guess from reduced set of characters, the words these sets could represent. Naturally not all people possess the same amount of vocabulary or command of a language and hence the figures he came up with, differ from figures we might find in literature, with similar tests conducted.
*7)
The Dutch alphabet consists of the same characters as the English alphabet and if we remove the German Umlaute and replace them with ae, oe, ue and the sharp s (ß) with ss, we can stay in the same 26 character alphabet. No German teacher conducting a test would dare to mark down a paper, because a student used instead of the umlaut two characters like for example ae. An umlaut and how it is written is permitted by two choices and neither of them is a mistake as far as correct writing goes.